Training

Batch Gradient Descent

Use the full training set at each Gradient Descent step

Pros

• Actually converge
• Sceles well with large number of features

Cons

• Slow on very large training sets

Stochastic Gradient Descent

picks a random instance in the training set at every step and computes the gradients based only on that single instance

Or, shuffle the training set, then go through it by instance, then shuffle it again, and so on, this generally converges more slowly

Pros

• Possible to train on huge training sets
• Has a better chance of finding the global minimum

Cons

• Final parameter values are good, but not optimal

Mini-batch Gradient Descent

Computers the gradients on small random sets of instance called mini-batches

Pros

• less erratic than SGD

Cons

• Harder to escape from local minima than SGD

Underfitting and Overfitting

	Training	Validation	Learning Curves		Solution
Underfitting	Poor	Poor	RMSE Values are high on the plateau	Adding more training examples will not help	Use more complex model or come up with better features
Overfitting	Well	Poor	RMSE values are low on the plateau	There is a gap between the curves	Feed more training data until the validation error reaches the training error

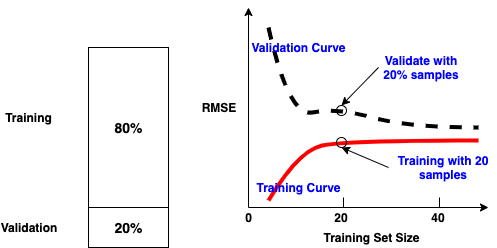
Three Errors

Bias

Due to wrong assumptions, a high-bias model is most likely to underfit the training data

Variance

Due to the model's excessive sensitivity, a model with many degrees of freedom is likely to have high variance, and thus to overfit the training data

Irreducible Error

Due to the noisiness of the data itself. The only way to reduce this part of the error is to clearn up the data

Bias-Variance Tradeoff

Increasing a model's complexity will typically increase its variance and reduce its bias. Conversely, reducing a model's complexity increases its bias and reduces its variance

Avoid Overfitting

• Reduce degrees of freedom
• Regulation
• Increase the size of the training set

Regulation

Ridge Regression

Add a regularization term equal to $\alpha \sum_{i=1}^{n}\theta_{i}^{2}$

• A model with regularization typically performs better than a model without any regularization

Lasso Regression

Add the regularizaiton term $\alpha \sum_{i=1}^{n} |\theta|$

• Automatically performs feature selection and outputs a sparse model, is good if only a few features actually matter, when you are not sure, prefer Ridge Regression
• behave erratically when the number of features is greater than the nubmer of training instances or when several features are strongly correlated

Elastic Net

Add the regularizaiton term $r\alpha\sum_{i=1}^{n}|\theta_{i}|+\frac{2}{1-r}\alpha\sum_{i=1}^{n}\theta_{i}^{2}$

• generally preferred over Lasso

Early Stopping

Stop training as soon as the validation error reaches a minimum A simple and efficient regularization techniques that Geoffrey Hinton called it a "beautiful free lunch."

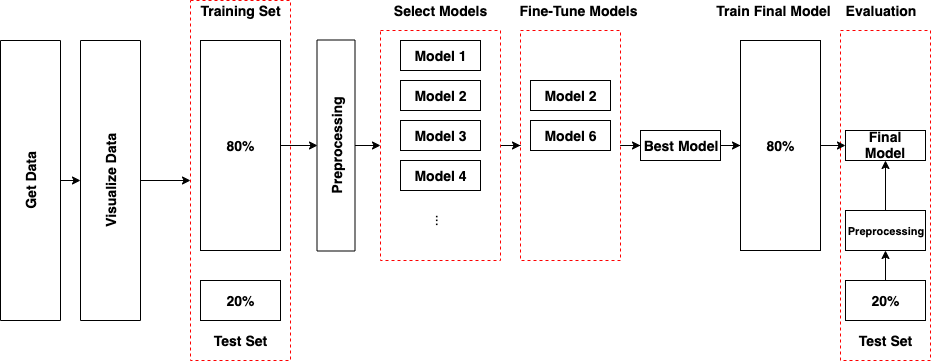
Testing and Validation

Reference

Hands-On Machine Learning with Scikit-Learn & TensorFlow

How to Train a Final Machine Learning Model