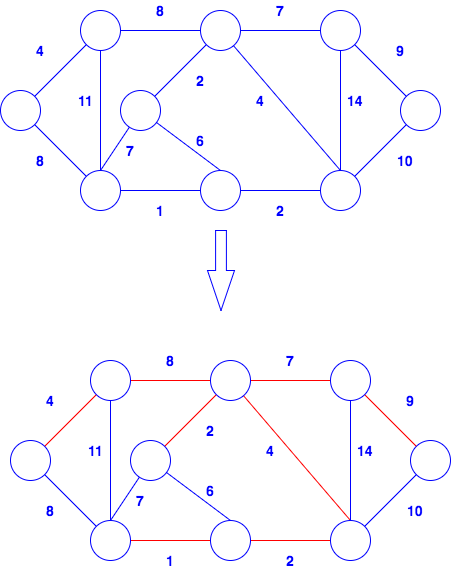
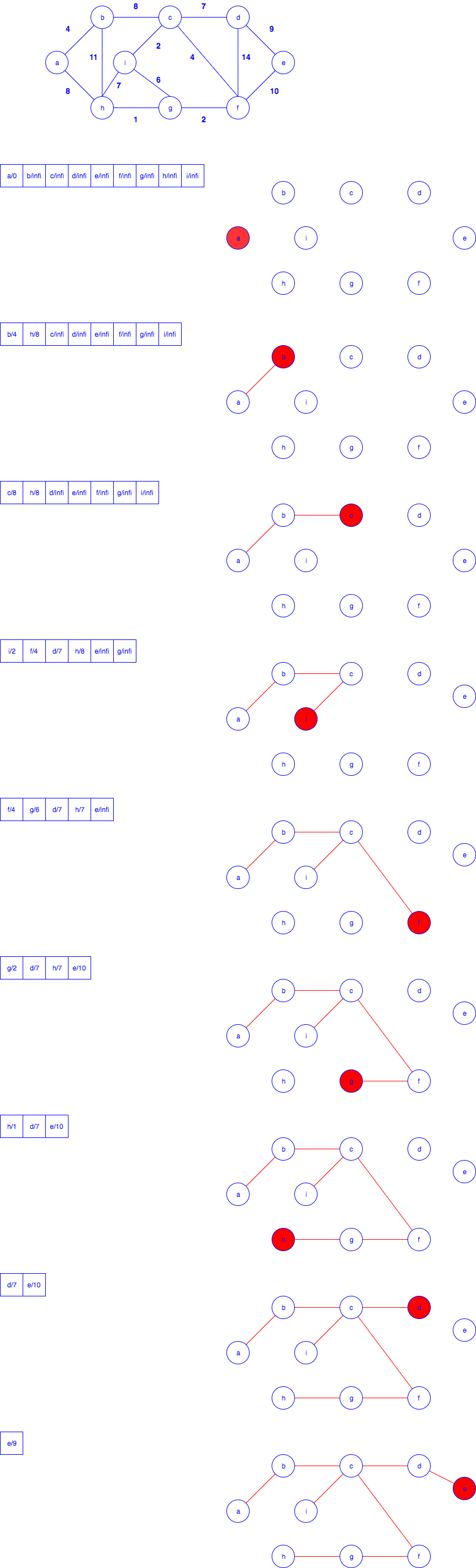
Minimum Spanning Tree
- For a undirected graph, fina an acylic tree spanning the graph with minimum total edge weight
Kruskal's Algorithm
- Set s1 = {a, b, c}, Set s2 = {d, e, f}, disjoint set
- Find-Set(x), find a set which contain element x
- Union(s1, s2), merge two sets
- O(ElgV)
- Create a set for each node
- Sort the edges by edge weights by nondecreasing order
- For each edge (u, v), if u and v are not in the same set, merge them, set the edge as tree edge of minimum spanning tree
Prim's Algorithm
- Each node has a key, which is the minimum weight of any edge connecting to it, the value is set as infinite initially
- Set up the key of the start node to be zero
- Each node has a pointer pointing to its parent in MST
- Push all nodes into a min-priority queue
- For each popped node, check all its neighbors and update its key value and parent, until the queue is empty
- O(ElgV)
Reference