Recursion
Recursion is a method of solving by breaking a problem down into smaller and smaller subproblems until it is small enough problem to be solved trivially
Base case, the simplest, smallest instance of the problem, that can’t be decomposed any further
Recursive step, decomposes a larger instance of the problem into one or smaller instances that can be solved by recursive calls, then recombines the results of those subproblems to produce the solution to the original problem
List Sum
Calculate the sum of a list of numbers
def summation(l):
if len(l) == 0:
return 0
if len(l) == 1:
return l[0]
return l[0]+summation(l[1:])
if __name__ == '__main__':
print(summation([]))
print(summation([1, 2, 3, 4]))
Convert Integer to a String in Any Base
Convert an integer to a string in some base between binary and hexadecimal
def convert(n, base):
convertString = "0123456789ABCDEF"
if n < base:
return convertString[n]
return convert(n//base, base) + convertString[n%base]
if __name__ == '__main__':
print(convert(10, 2))
print(convert(769, 10))
print(convert(1000, 16))
Reverse String
Get a new string that is the reverse of the old string
def reverse(s):
if len(s) <=1:
return s
return s[len(s)-1] + reverse(s[1:(len(s)-1)]) + s[0]
if __name__ == '__main__':
print(reverse('abc'))
Palindrome
Returns True if the string is a palindrome
import string
def isPalindrome(s):
if len(s) <= 1:
return True
if s[0] != s[len(s)-1]:
return False
else:
return isPalindrome(s[1:(len(s)-1)])
def remove_space_punctuation(s):
return s.translate(str.maketrans('', '', ' '+string.punctuation))
if __name__ == '__main__':
print(isPalindrome('kayak'))
print(isPalindrome(remove_space_punctuation('Reviled did I live, said I, as evil I did deliver').lower()))
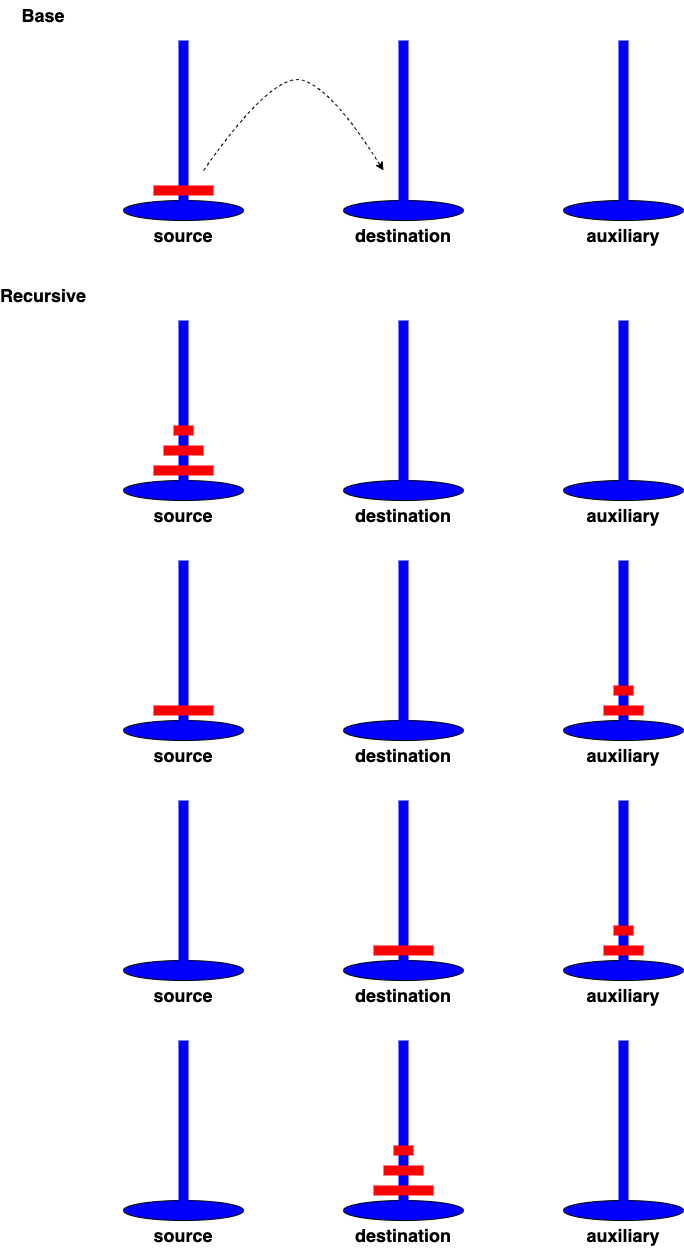
Tower of Hanoi
Move all the disks from source to destination without violating the sequence of arrangement. A few rules to be followed for Tower of Hanoi are:
- Only one disk can be moved among the towers at any given time
- Only the "top" disk can be removed
- No large disk can sit over a small disk
def hanoi(n, source, dest, aux):
if n >= 1:
hanoi(n-1, source, aux, dest)
print('Move from '+source+' to '+dest)
hanoi(n-1, aux, dest, source)
if __name__ == '__main__':
hanoi(2, 'source', 'dest', 'aux')
Reference